İlkokul 4. sınıf matematik dersi Matematik Eşitlikte Verilmeyen Sayıyı Bulma konu anlatımını bu sayfada bulabilir ve pdf olarak indirebilirsiniz.
MATEMATİKSEL EŞİTLİKTE VERİLMEYEN SAYIYI BULMA
BU KONUDA NELER ÖĞRENECEĞİZ?
→ Matematiksel eşitlikte verilmeyen sayıyı bulma
→ Matematiksel ifadeleri eşitlik hale getirme
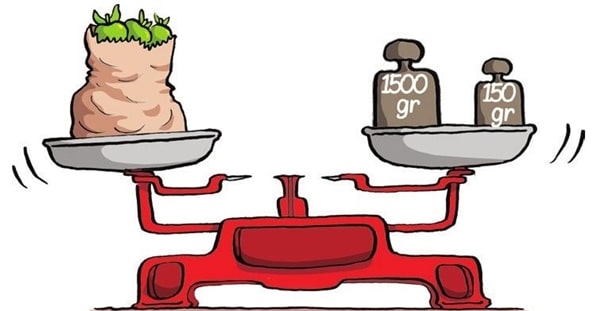
Yukarıdaki terazinin dengede olduğunu görüyoruz. O halde meyveler 1650 grama eşittir.
Dengede duran bir terazinin iki kefesindeki kütle miktarının eşit olması gibi matematiksel ifadelerin arasında = işareti varsa her iki taraftaki işlemlerin sonucu birbirine eşittir.
Eşitlik durumu “=” ile, eşit olmama durumu “≠” sembolü ile gösterilir.
Eşitlikte Verilmeyen Sayıyı Bulma
Aralarında eşitlik durumu olan iki matematiksel ifadeden birinde verilmeyen değer olabilir. Verilmeyen değer bulunurken ifadelerin birbirine eşit olduğu dikkate alınmalıdır.

ÖRNEK: Yukarıda verilen terazideki sarı cismin kütlesini bulalım.
Terazinin sol kefesinde 1 adet yeşil ve 4 adet mavi cisim var. Sağ kefesinde ise iki adet mavi ve bir adet turuncu cisim var. Denge durumunu belirten eşitliği yazalım.
Sol Kefe = Sağ Kefe
1 + 1 + 1 + 1 + 3 = 1 + 1 + ?
7 = 2 + ?
2 ile 5‘in toplamı 7 eder. O halde sarı cismin kütlesi 5 kg‘dir.
ÖRNEK: A ÷ 12 = 54 × 2 eşitliğinde A yerine yazılması gereken sayıyı bulalım.
A ÷ 12 = 54 × 2
A ÷ 12 = 108
12‘ye bölümü 1296‘dır. A = 1296
İfadeleri Eşit Hale Getirme
Aralarında eşitlik durumu olmayan iki matematiksel ifadenin eşit olması için denge durumu sağlanmalıdır. Ya da işlemlerin sonuçları eşitlenmelidir.
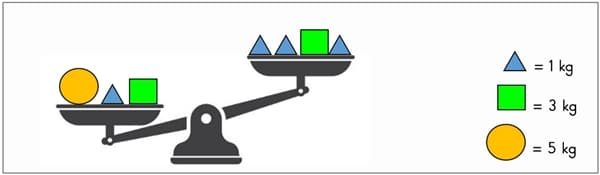
ÖRNEK: Dengede olmayan yukarıdaki terazideki kütleler verilmiştir. Terazinin dengeye getirilmesi için yapılması gerekenleri yazalım.
Sol Kefe ≠ Sağ Kefe
5 + 3 + 1 ≠ 3 + 1 + 1+ 1
9 ≠ 6
Terazinin dengeye gelmesi için sol kefesinden yeşil cisim alınmalıdır veya sağ kefesine bir adet yeşil cisim konulmalıdır.
4. sınıf Matematiksel Eşitliklerde Verilmeyen Sayıları Bulma konusunu pekiştirelim.
4. Sınıf İfadelerin Eşitliği Kazanımları
M.4.1.5.7. Aralarında eşitlik durumu olan iki matematiksel ifadeden birinde verilmeyen değeri belirler ve eşitliğin sağlandığını açıklar.
Örneğin 8 + ![]() = 15 – 3 12 : 4 =
= 15 – 3 12 : 4 = ![]() + 1 6 x
+ 1 6 x ![]() = 48 – 12
= 48 – 12
M.4.1.5.8. Aralarında eşitlik durumu olmayan iki matematiksel ifadenin eşit olması için yapılması gereken işlemleri açıklar.
Örneğin 8+5 ≠ 12-3 ifadesinde eşitlik durumunun sağlanabilmesi için yapılabilecek işlemler üzerinde durulur.
4. Sınıf İfadelerin Eşitliği Etkinlikleri
| Önceki Konu Anlatımı | Sonraki Konu Anlatımı |
| Çarpma Bölme İlişkisi | Kesir Çeşitleri |
